Graphs of Renewable Performance in South Africa in August/September 2024
The graphs in this post were prepared using data available from Eskom's Data Portal.
Introduction
Data on the performance of Renewables available from Eskom’s Data Portal is downloaded at the beginning of every month then analysed and graphed for the month just passed and the month before that. This dataset supplies values for every hour of the 24 in a day for every day in a period selected. (The Glossary will allow you to discover that “Other RE” encompasses “Generation from other smaller contracted renewables (small hydro, biomass, landfill gas, etc.)”).
For the purposes of comparison, standardization, I calculate the ratio of production by a generator (Wind, PV, Nuclear, whatever) to the maximum potential production of that generator for every hour of the day by that generator. This is the basis of the definition of the “Capacity Factor”, CF, of a generator, but I prefer to calculate the CF for a longer period, my preference being a full year (year-to-date). For this reason, I will refer to the amount calculated from Eskom’s data as the “Hourly Capacity Factor”. The average of these values in the period is reported as the “CF for the period”.
The Eskom dataset does not include an “Installed Capacity” value for nuclear. My initial guess for this value is 969 MW per unit, a total of 1938 MW for Koeberg after refurbishment of both units. For Wind, PV and so an, the dataset contains pairs of values; a production value in the hour of the day concerned and the “Installed Capacity: of the generator concerned. My analyses are based on the ratio of the numbers in a pair - with 1938 MW the guessed value of the divisor for Koeberg.
I include nuclear under the definition of “renewable” because the point of “fuel” being “renewable” is that it will not run out until the sun burns out (when humanity is extinguished). This characteristic is shared by nuclear fuel. True, it’s consumed but the amount of uranium and thorium available (known reserves) would last humanity for the life of Earth. This is normally described by the term “sustainable” and there is no doubt that renewables (the conventional definition) and nuclear are sustainable.
Graphs
The graphs in this section reflect the resolution of the data. If there are 60 days in the two months concerned then, horizontally, 60×24 = 1440 pixels are used to allocate a pixel for the value of the CF recorded for every hour in the two months concerned. Vertically, 800 pixels are allocated to represent 100%, so 8 pixels for 1% or one-eighth of a percent (0.125%) per pixel.
PV
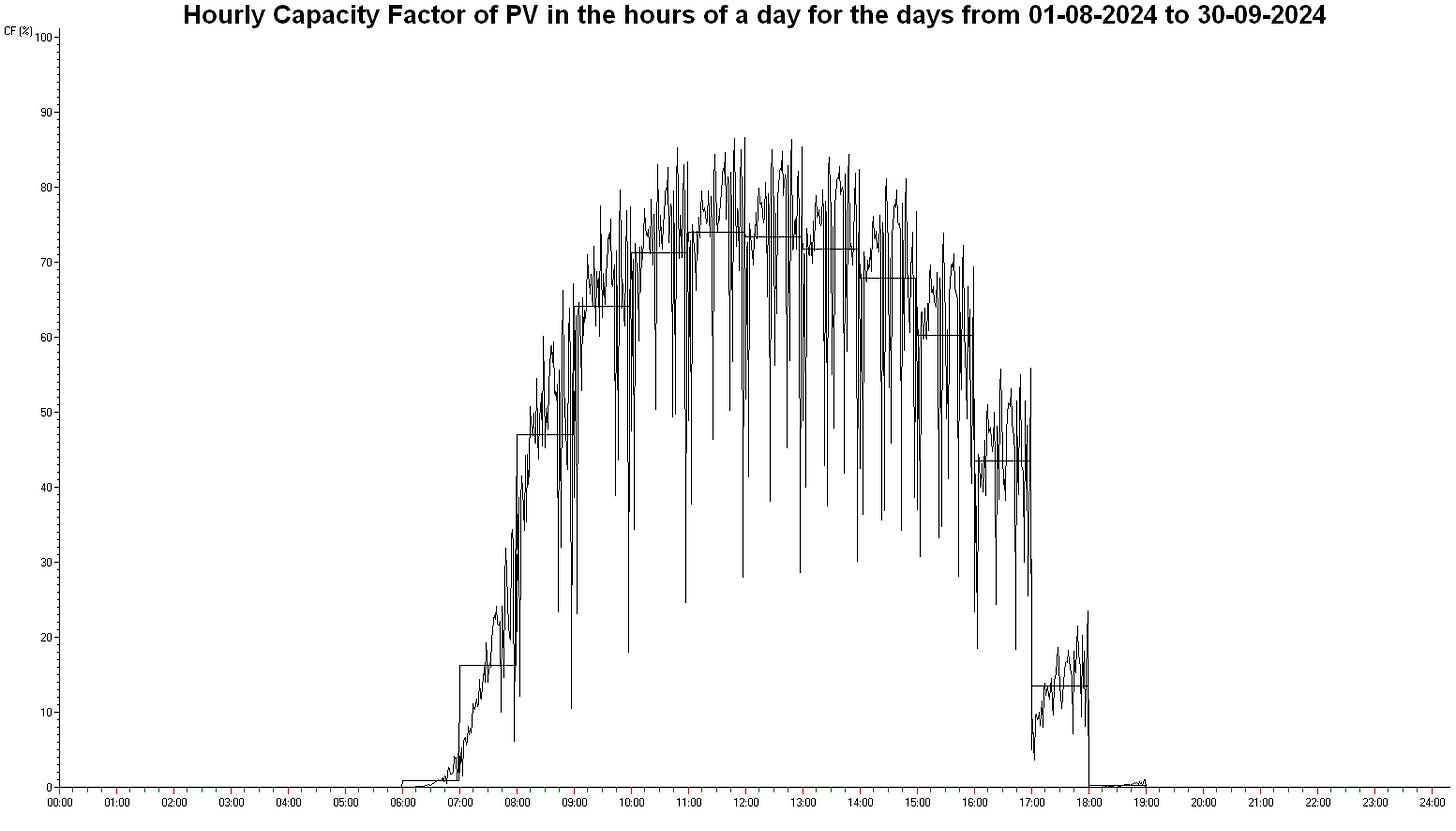
The installed capacity was 2287.09 MW throughout the period. The Capacity Factor in the period was 25.1639%.
Wind
The installed capacity was 3442.57 MW throughout the period. The Capacity Factor in the period was 41.2603%.
CSP
The installed capacity was 500 MW throughout the period. However, reports indicate that the Redstone plant (100 MW) was synchronized to the grid on or around the 15th of September. I will leave the installed capacity at 500 but if there’s an error, the result is an over-statement of the capacity factor. This was 25.5092% in the period.
Other RE
The installed capacity was 50.58 MW throughout the period. The Capacity Factor in the period was 68.0561%.
All RE
The installed capacity was 6280.240 MW throughout the period (possibly 6380.24 - see the details for CSP above). The Capacity Factor in the period was 34.3602%. This plot includes PV, Wind, CSP and Other RE (all the generators reported above).
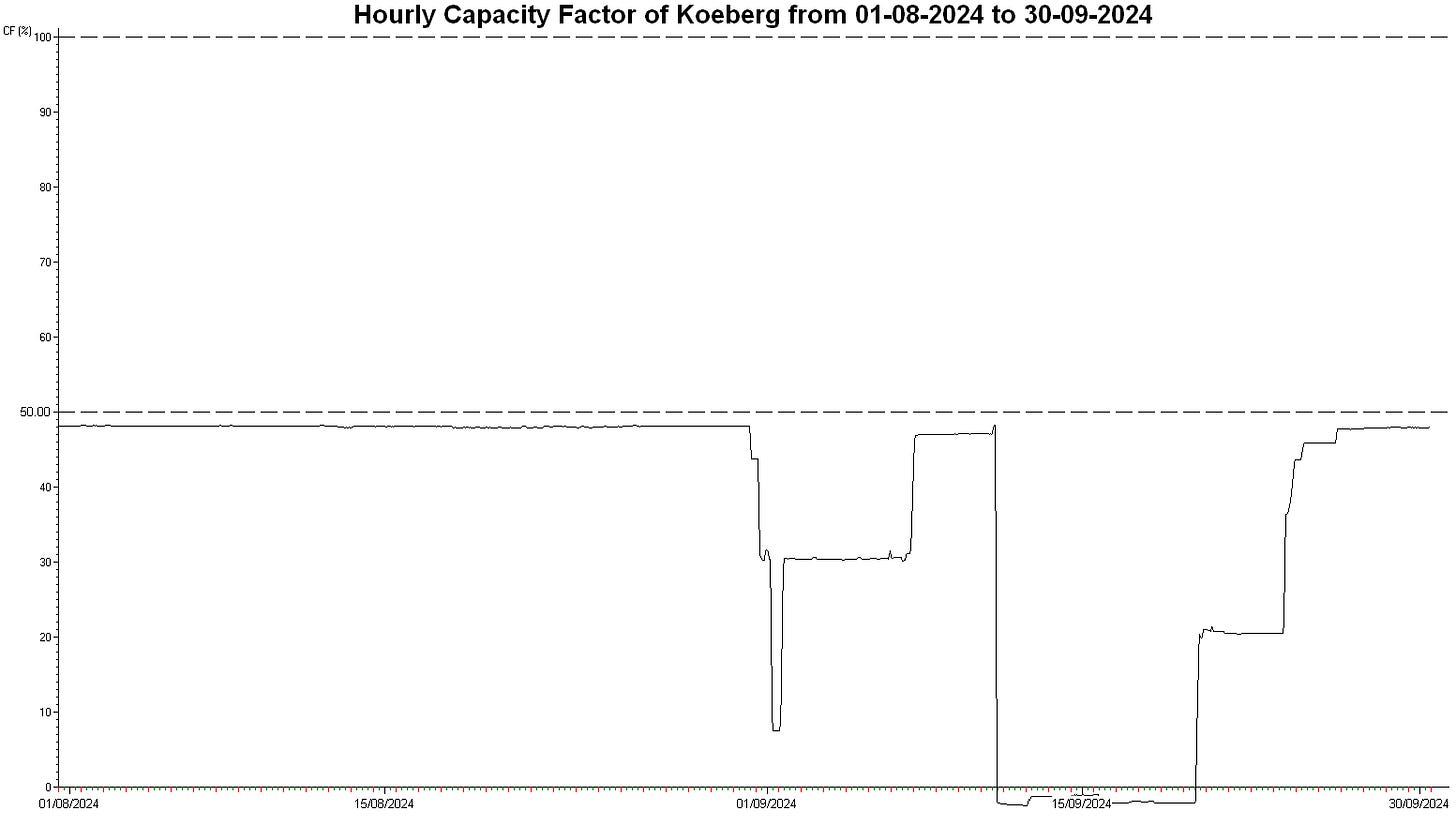
Nuclear (Koeberg)
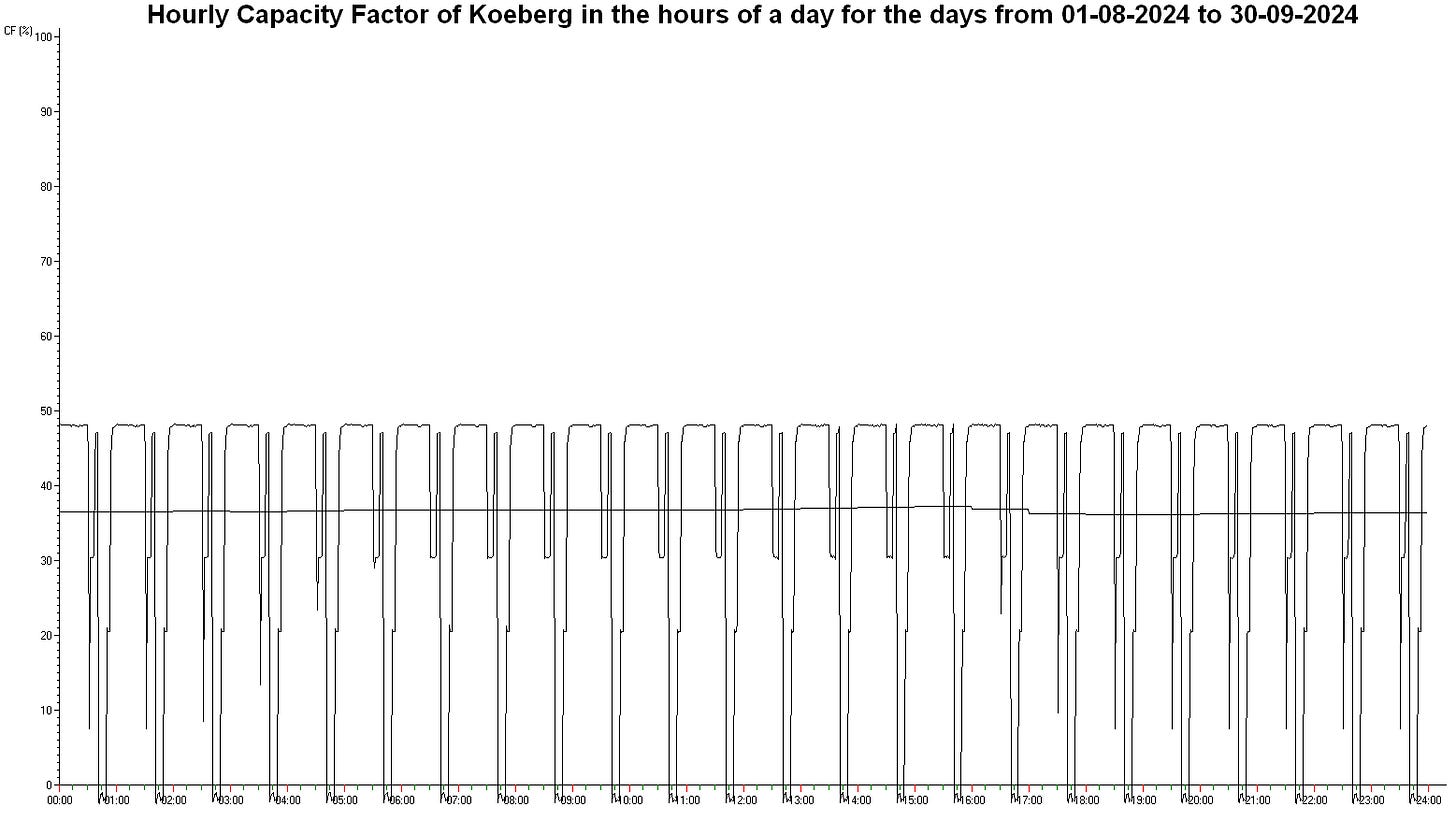
While Unit 2’s refurbishment continues, Koeberg is outputting only half its potential. My guessed value of 969 MW per unit is contradicted by the maximum observed output in the period from 01/01/2024 to 30/09/2024 of 955.014 MW. The Capacity Factor in the period was 36.6238%. Unit 1 went down for about 9 days in September, resulting in the negative output plotted. The biggest negative number (i.e, the smallest value) was -47.584 MW. Nuclear plants require an energy input (normally produced by the plant’s reactor or reactors) in their operation.
A variations on the graphs above
The graphs above plot time along the x-axis; successive days are plotted with the hours of the day, from midnight, through midday to midnight. In the plots below the sequence is rearranged with the hours of the day as the primary sequence and the days in the period as a secondary sequence. This allows an average for the hours of the day to be plotted as an overlay.
PV
Wind
CSP
Other RE
All RE
Nuclear (Koeberg)
Numerical Analysis
Humanity has decided that (if one is to understand the message on display in just about every news outlet I encounter) the use of fossil fuels to generate the majority of the energy consumed (80% in 2024) is a destructive practice and that alternatives must be found. Listen closely and I hear that “renewables” (the definition excluding nuclear power) must have replaced fossil fuels by 2050; or 2018 + 12 = 2030; in a phrase, “very rapidly”. I decided to produce a monthly report to analyse the performance of “renewables” (including nuclear power) in South Africa.
My decision was based on opinions I was encountering which state that “renewables” (excluding nuclear) cannot replace “fossil fuels” (a class which includes “natural gas”, gas recovered from terrestrial resources which consists mainly of methane; burning such materials has carbon dioxide, CO₂, as a waste product). Only “renewables” can, the opinion concludes.
This opinion is countered by the opinion that “renewables” (which, in South Africa, largely excludes hydro-electric power, which for the most part will be wind turbines and varieties of solar power - PV, trough CSP and tower CSP) are too intermittent (they produce only when Mother Nature is smiling) to be reliable. No modern industrialized nation on Earth has ever been powered by “Wind, Water an Sun” (“the 100% WWS opinion”) although some rely mainly on hydropower and/or geothermal power for their electricity supply. (The term “power” includes the fuel for industrial processes, home heating and transport, both on roads and in the air and on the sea, etc - power consumption which might be dependent on electricity but which is currently not electrical at the point of consumption.)
Challenge the 100% WWS opinion, pointing at regions without benefit of hydropower (“water”) or geothermal power (for example, those without the benefits available to Iceland) which experience long periods with insufficient power from wind and solar to power society, and the response is “storage”. This word refers to a variety of solutions, from Pumped Hydro Storage through “batteries” (mainly Li-ion batteries) to Gas-To-Power (GTP) applications. But whatever the word means, it implies a backup system which is to be used only when the primary system is failing. The cost of such the system duplication needs to be properly accounted for. So far, I’ve seen little attempt at honest accounting. The cost of capital invested on equipment standing idle (because the primary system is functioning adequately - or because the primary system is insufficient) appears not to be relevant to those with 100% WWS aspirations.
I decided to produce the graphs offered above because I believe a graph is “data at a glance”. I don’t expect you to wade through the thousands of values in Eskom’s dataset so that you might form an opinion. I’m offering you graphs produced from that dataset which, at a glance, should supply you with the information in the dataset.
Another method of presenting the information a dataset is to offer a limited numbed of summary statistics. The obvious first choice is the arithmetic mean - which is a measure of the typical value in a collection of data values. However an obvious characteristic of almost all data sets is that the values are not uniformly one value - there is variation, a deviation from the average value. A measure of the typical size of this deviation is the standard deviation, SD. For ratio scale variables, the coefficient of variation, CV, combines these two values and is in itself a useful measure. For more details, see my post on the CV.
Two aspects of the graphs above is striking. For all generators there is a clear tendency during the course of a day - and for all generators there is some degree of variation about the typical value for a day. These two sources of variation may be evaluated and contrasted in a standard tool known as a One Way Analysis of Variance (or, briefly, a One Way ANOVA). For more details, see this post. I’ve reported this analysis up to the level of the F-ratio, the ratio of the Mean Square Between Hours to the Mean Square Within Hours but the measure cannot be easily used in the manner it is normally used. In this analysis it merely contrasts the two sources of variation. It is to be used when comparing generators.
The summaries follow.
PV
Wind
CSP
Other RE
All RE
Nuclear (Koeberg)
Summary
Presenting summary statistics in a single table facilitates comparison.
Interestingly, Koeberg, with one unit being refurbished (with one hand tied behind it’s back, so to speak) and with the other unit producing no electricity (consuming electricity) for roughly one-third of the month, still managed a better CF (36.6%) than All RE (34.4%) and the lowest coefficient of variation (49.4%) and F-ratio (0.0003) of all the technologies.